工場裏のアーカイブス

素人によるiPhoneアプリ開発の学習記　あと機械学習とかM5Stackとか

統計学の備忘録的な学習メモ（2）

Python 雑記

統計学の備忘録的な学習メモ（1）に引き続き、Python（Scipyなど）を用いた統計学の勉強に関するメモです。（2）では主に様々な分布および検定についてまとめています。

個人的な備忘録の意味合いが強く、他記事と書き方が異なっており、説明なども少なめです。今後は予告なく内容を追加・修正するかもしれません。

※環境はJupyter Notebookの想定です。

　

インポートするライブラリ

import numpy as np
import pandas as pd
import scipy as sp
from scipy import stats
from scipy.special import gamma

from matplotlib import pyplot as plt
import seaborn as sns
sns.set()

　

二項分布のプロット

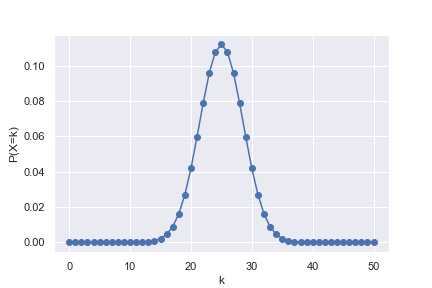
公正なコイン（きちんと表、裏がそれぞれ1/2の確率で出る）を50回投げて、そのうち表がk回出る確率をプロット。

n = 50 #試行回数
p = 1/2 #確率
k = np.arange(0, n + 1, 1)

#試行回数n回のうち、確率pの事象がk回起こる確率
#離散的なデータなので、pdfではなくpmf関数となる
pk = stats.binom.pmf(k, n, p)

#二項分布を折れ線としてプロット
plt.plot(k, pk, marker='o')
plt.xlabel("k")
plt.ylabel("P(X=k)")
plt.show()


　

二項分布を用いた検定

コインを20回投げたら表が15回出たとき、コインが公正と言えるかを検定する。

print(stats.binom_test(15, 20, 1/2)})

結果はおよそ0.0414となり、5%有意水準（0.05）では「コインが公正である」という帰無仮説は棄却される。

別の方法で確認する。表が5回以下となる確率、15 回以上となる確率をそれぞれ求める。当然ながら両者は一致し、またこれらの和が先程の0.0414と一致することが確認出来た。

lower = stats.binom.cdf(5, 20, 1/2) #公正なコインの表が、20回中0〜5回出る確率
upper = 1 - stats.binom.cdf(14, 20, 1/2) #公正なコインの表が、20回中15〜20回出る確率

print(f'lower = {lower:.4}')
print(f'upper = {upper:.4}')
print(f'upper + upper = {lower + upper:.4}')

lower = 0.02069
upper = 0.02069
upper + upper = 0.04139

　

t分布のプロット

さまざまな自由度（df）におけるt分布の形をプロットしてみる。標準正規分布も併せてプロットする。

df_array = np.arange(1, 10, 1)

fig = plt.figure(figsize=(10, 5))
ax = fig.add_subplot(111)
x = np.linspace(-4, 4, 100)
for i in range(0, len(df_array)):
    y = stats.t.pdf(x, df=df_array[i])
    ax.plot(x, y, label=f'df = {df_array[i]}', alpha=0.6)
ax.plot(x, stats.norm.pdf(x), label='norm', alpha=0.6)
ax.set_xlabel('t or z')
ax.set_ylabel('probability density')
plt.legend()


自由度の値が大きくなるほど、標準正規分布（norm表記）に近づくことが確認出来た。

　

t分布を用いた母平均の区間推定

あるサンプルについて、母集団の平均の95%信頼区間を推定する。

sample = np.array([10.1, 9.8, 11.1, 10.5, 9.6, 10.8])
mu = sp.mean(sample)
print(f'標本平均 = {mu:.4}')
sigma = sp.std(sample, ddof=1) #不偏分散の平方根

df = len(sample) - 1 
print(f'自由度 = {df}')
se = sigma/sp.sqrt(len(sample)) #標本標準誤差

interval = stats.t.interval(alpha = 0.95, df = df, loc = mu, scale = se)
print(f'下側信頼限界 = {interval[0]:.4}')
print(f'上側信頼限界 = {interval[1]:.4}')

標本平均 = 10.32
自由度 = 5
下側信頼限界 = 9.703
上側信頼限界 = 10.93

　
別の方法でも確認する。t.ppf()関数を用いて2.5%点、97.5%点を自分で計算し、信頼限界を求めてみる。

#mu、se、dfは先程の例と同じであるとする
#※t分布は対称形なので、t_975 = -t_025と求めることも出来る
t_025 = stats.t.ppf(q = 0.025, df = df) 
print(f’2.5%点 = {t_025:.4}') 
t_975 = stats.t.ppf(q = 0.975, df = df)
print(f'97.5%点 = {t_975:.4}') 

print(f'下側信頼限界 = {mu + t_025 * se:.4}')
print(f'上側信頼限界 = {mu + t_975 * se:.4}')

信頼区間は先程と確かに一致することが確認出来た。

2.5%点 = -2.571
97.5%点 = 2.571
下側信頼限界 = 9.703
上側信頼限界 = 10.93

※なお信頼区間の正しい解釈は中々難しい。今回の結果を「母平均の値は95%の確率で、9.703〜10.93の間に存在する」と考えるのは正しくない模様（母平均の真の値は知るのが困難だけで、あらかじめ確定した定数であり、信頼区間の間に存在する/しないは本来はっきり定まっているため、95%の確率で存在する…という考え方は出来ない）

正しい解釈は、また別のサンプルを母集団から同様の手順で抽出して、信頼区間の推定を行う…という手順を100回繰り返した場合、そのうち95回は信頼区間の間に母平均の値が存在する、という具合のようです。以下のサイトが参考となりました。

19-3. 95％信頼区間のもつ意味 | 統計学の時間 | 統計WEB

　

1群のt検定

例えば、平均厚み50 mm狙いで量産されている製品について、サンプルを10個抽出して厚みを実測したところ、以下の表のようになった（標本平均 50.67）。

50.2 51.4 49.7 51.1 49.4 50.9 52.1 51.4 50.9 49.6

この製品の平均厚みは本当に50 mmであると言えるか？。1群のt検定ではこうした問題に対する判断を行うことが出来る。有意水準は5%とする。

sample = np.array([50.2, 51.4, 49.7, 51.1, 49.4, 50.9, 52.1, 51.4, 50.9, 49.6])

mu = sp.mean(sample)
print(f'標本平均 = {mu:.4}')

df = len(sample) - 1
print(f'自由度 = {df}')

sigma = sp.std(sample, ddof=1) #不偏分散の平方根
se = sigma / sp.sqrt(len(sample)) #標本標準誤差

t_value = (mu - 50)/se #母平均は50という仮定に基づく
print(f't値 = {t_value:.4}')

alpha = stats.t.cdf(t_value, df = df) #標本のt値を、t分布がを下回る確率
print(f'α = {alpha:.4}')
print(f'p値 = {(1 - alpha) * 2:.4}') #両側検定なので *2 となる

#stats.t.sf(t_value, df = df) #t.sf関数（生存関数）を用いれば、(1-alpha)の値が直接求まる。

p値が約0.043となり、有意水準5%（0.05）を下回った。サンプルの平均厚みは50 mmとは有意に異なると言える。

標本平均 = 50.67
自由度 = 9
t値 = 2.349
α = 0.9783
p値 = 0.04337

　
1群のt検定は、専用の関数を用いてもっと簡単に行うことも可能である。

#sampleは先程の例と同じであるとする
t_value, p_value = stats.ttest_1samp(sample, 50)
print(f't値 = {t_value:.4}')
print(f'p値 = {p_value:.4}')

t値、p値は確かに先程の例と一致している。

t値 = 2.349
p値 = 0.04337

　
母集団（すなわち製品全体）の平均厚みについて、信頼区間の推定も行ってみる。

#mu、se、dfは先程の例と同じであるとする
interval = stats.t.interval(alpha = 0.95, df = df, loc = mu, scale = se)
print(f'下側信頼限界 = {interval[0]:.4}')
print(f'上側信頼限界 = {interval[1]:.4}')

信頼区間は50.02〜51.32となり、50を含まないことが確認出来た。

下側信頼限界 = 50.02
上側信頼限界 = 51.32

　

対応のある2群のt検定

例えば、5人の被験者（A〜E）について、異なる状態1、2における心拍数を測定した結果を測定した結果、以下の表のようになった。

A B C D E
状態1 105 99 94 88 110
状態2 96 93 87 90 102

状態1と2の違いが、心拍数に影響を及ぼしているだろうか？2群のt検定ではこうした問題に対する判断を行うことが出来る。有意水準は5%とする。

今回は同じ被験者に対するデータなので、状態1、2のデータはペアとして考えることが出来る。この場合は対応のある2群のt検定を行う。まず状態1、2の差分を取って、差分に対して平均が0となるかどうか、1群のt検定を行えば良い。

data = pd.DataFrame({
    'person' : ['A','B','C','D','E','A','B','C','D','E'],
    'state' : ['S1','S1','S1','S1','S1','S2','S2','S2','S2','S2'],
    'heart_rate' : [105, 99, 94, 88, 110, 96, 93, 87, 90, 102],
})

#状態(state)別の、心拍数の数値データを抜き出す
state1 = np.array(data.query('state == "S1"')['heart_rate'])
state2 = np.array(data.query('state == "S2"')['heart_rate'])

#状態1、2の差分を計算する
diff = state1 - state2

#差分に対して、母平均が0と異なるか否か、1群のt検定を行う
#0と異なると言える場合は、状態1、2における心拍数は有意に異なると言える
t_value, p_value = stats.ttest_1samp(diff, 0)
print(f't値 = {t_value:.4}')
print(f'p値 = {p_value:.4}')

p値は約0.046となり、有意水準5%（0.05）を下回った。状態1と2の違いは、有意に心拍数に影響を及ぼしていると言える。

t値 = 2.85
p値 = 0.04638

　
対応のある2群のt検定も、専用の関数で簡単に行うことが可能である。結果は先程と全く同じとなる。

t_value, p_value = stats.ttest_rel(state1, state2)
print(f't値 = {t_value:.4}')
print(f'p値 = {p_value:.4}')

　

対応のない2群のt検定（Welchのt検定）

例えば、異なるクラスにおけるテストの平均点の比較、異なる工場で作られた同種製品の平均サイズの比較など、それぞれ独立したデータ同士には対応のない2群のt検定を適用する。

この場合、「かつては」2群の分散が等しいか異なるかをまず判定し（F検定で行う）、それによって2通りの方法を使い分ける必要がある、という考えが主流であったとのこと。しかし最近では…

  • 分散が異なる場合用とされていた方法（Welchのt検定）は、分散が等しい場合に適用しても支障がないこと
  • F検定 → t検定　の2段階を経ると、多重性の問題が生じること

といった理由によって、最初からWelchのt検定を行う考えが主流になっているとのことである。

【参考となった外部サイト】
等分散検定から t検定，ウェルチ検定，U検定への問題点
検定の多重性を分かりやすく解説します【F検定⇒t検定はダメ？】
24-4. 対応のない2標本t検定 | 統計学の時間 | 統計WEB

先程の心拍数のデータを、対応のないデータと仮定して、Welchのt検定を試してみる。

#equal_var = Falseとすると、分散が異なる2群向けのWelchのt検定が適用される
#本文で記載した通り、常にWelchのt検定でも支障がないとのこと
t_value, p_value = stats.ttest_ind(state1, state2, equal_var = False)
print(f't値 = {t_value:.4}')
print(f'p値 = {p_value:.4}')

使用データ自体は先程と同じだが、結果はもちろん異なっている。p値が約0.270となり有意水準5%（0.05）を上回っているので、有意差が得られないという結論となる。

t値 = 1.199
p値 = 0.2697

　
確認のために、Welchのt検定の式に従って自力でも計算してみる。state1、2の標本サイズをn_1, n_2、標本平均を\bar{x}_1, \bar{x}_2、不偏分散を\hat{\sigma}_1, \hat{\sigma}_2とすると、t値は以下の式で計算出来る。
t = \frac{\bar{x}_1 - \bar{x}_2} {\sqrt{\frac{\hat{\sigma}_1^2}{n_1} + \frac{\hat{\sigma}_2^2}{n_2}}}

自由度\nuは以下の式で近似的に求めることが出来る。
\nu \approx \frac{\left( \frac{\hat{\sigma}_1^2}{n_1} + \frac{\hat{\sigma}_2^2}{n_2} \right)^2} {\frac{\hat{\sigma}_1^4}{ n_1^2 \left( n_1 - 1 \right)} + \frac{\hat{\sigma}_2^4}{ n_2^2 \left( n_2 - 1 \right)}} 

mean1 = state1.mean()
mean2 = state2.mean()
var1 = state1.var(ddof=1)
var2 = state2.var(ddof=1)
n1 = state1.size
n2 = state2.size

t_value = (mean1 - mean2) / np.sqrt((var1/n1 + var2/n2))
print(f't値= {t_value:.4}')

df = (var1/n1 + var2/n2)**2 / (var1**2/(n1**2*(n1 - 1)) + var2**2/(n2**2*(n2 - 1)))
alpha = stats.t.cdf(t_value, df = df)
print(f'p値 = {(1-alpha)*2:.4}')

結果は先程ときちんと一致することが確認出来た。

t値 = 1.199
p値 = 0.2697

　

母比率の区間推定

例えば、無作為に選んだ100人に好きなプログラミング言語のアンケートを実施したところ、15人がPythonと答えたとする（比率：15/100 = 0.15、15%）。ここから、世の中におけるPython好きな人の比率について、95%信頼区間を推定してみる。これは母比率の区間推定であり、binom.interval関数を用いれば簡単に行うことが出来る。

sample_size=100 #サンプルサイズ
prop = 0.15 #比率（標本比率）

interval = stats.binom.interval(alpha = 0.95, n = sample_size, p = prop)

#intervalには比率ではなく数（この場合はPython好きな人数の下限値、上限値）が返されることに注意.
#比率に直すには、サンプルサイズで割る必要がある.
print(f'下側信頼限界 = {interval[0]/sample_size:.4}') 
print(f'上側信頼限界 = {interval[1]/sample_size:.4}')

結果は以下の通りであり、Python好きな人の比率の95%信頼区間は、0.08〜0.22（8%〜22%）となる。標本平均15%に対して±7%の幅を持つことになる。

下側信頼限界 = 0.08
上側信頼限界 = 0.22


別の方法でも確認する。binom.ppf()関数を用いて2.5%点、97.5%点を自分で計算し、信頼限界を求めてみる。結果は先程の例と全く同じであり、2.5%点、97.5%点はそのまま、Python好きな人数の下限値、上限値である。

#sample_size, propは先程の例と同じとする
p_025 = stats.binom.ppf(q=0.025, n=sample_size, p=prop)
p_975 = stats.binom.ppf(q=0.975, n=sample_size, p=prop)

print(f'下側信頼限界 = {p_025/sample_size:.4}')
print(f'上側信頼限界 = {p_975/sample_size:.4}')

　

母比率の区間推定に向けたサンプルサイズの決定

先程の例では標本比率15%に対して、95%信頼区間は±7%の幅を持つという結果となった。

ここで逆に、95%信頼区間の幅を確実に±2%以内に収められるよう、サンプルサイズ（アンケート対象とする人数）を決定したいとする。母比率をp、標本比率を\hat{p}、サンプルサイズをn、信頼係数を\alphaとすると、信頼区間は以下の式で求められる。

\hat{p} - z \times \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} < p < \hat{p} + z \times \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}

ただしzは\alphaに対応する標準正規分布の値である。\alphaが95%の場合、zは標準正規分布の2.5%点（または97.5%点）である1.96となる。

式より、z \times \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}の部分の値が、まさに±何%となるかの幅そのものとなる。95%信頼区間の幅を±2%（0.02）以内に収めるために必要なサンプルサイズは、以下の式をnについて解けば求められる。

1.96 \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} = 0.02

実際に解くと以下の通りとなる。

n = \left( \frac{1.96}{0.02} \right)^2 \hat{p}(1-\hat{p})

ただし先程の例で\hat{p}は15%（0.05）であったが、これは実際に100人にアンケートをした結果の値である。しかしここでは、アンケートを行う前に対象人数を決定したい状況を想定しているため、\hat{p}はまだ未知の値である。

そこで1つの方法として\hat{p} = 0.5と仮定する。これは\hat{p}(1-\hat{p})の部分が最大となり、必要なサンプルサイズが最多となるワーストケースとなってしまうが、その場合でも±2%に収まれば確実に目的を達成できる。実際に計算を試してみた。

alpha = 0.95 #信頼係数. 
prop = 0.5 #標本比率だが, 今回は未知であるので, ワーストケースの0.5と仮定
scope = 0.02 #信頼区間の幅を, ±何%以内に収めたいかの値

#norm.ppf関数が負の値を返す場合でも、二乗しているので、問題なく計算できる
sample_size = (stats.norm.ppf((1 - alpha)/2) / scope)**2 * prop * (1 - prop)

#サンプルサイズは整数なので、丸めて表示する
print(f'必要なサンプルサイズ:{round(sample_size)}')


結果は以下の通りであり、最低でも2401人にアンケートを取れば良いことが分かる。

必要なサンプルサイズ:2401

また別の方法として、\hat{p}の値を仮定してしまうことも考えられる。例えば過去の知見から、比率が20%を超えることはまず無い、などと見積もれる場合は、ワーストケースとして\hat{p} = 0.2を仮定すれば良い（上記のコードで、prop = 0.2とする）。この場合の必要人数は1537人と、より少なくなる。

　

カイ二乗分布のプロット

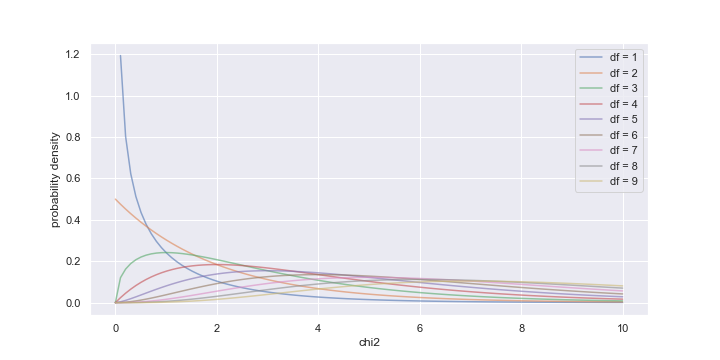
さまざまな自由度（df）におけるカイ二乗分布の形をプロットしてみる。

df_array = np.arange(1, 10, 1)

fig = plt.figure(figsize=(10, 5))
ax = fig.add_subplot(111)
x = np.linspace(0, 10, 100)
for i in range(0, len(df_array)):
    y = stats.chi2.pdf(x, df=df_array[i])
    ax.plot(x, y, label=f'df = {df_array[i]}', alpha=0.6)
ax.set_xlabel('chi2')
ax.set_ylabel('probability density')
plt.legend()


　

カイ二乗分布のシミュレーション

正規分布に従う母集団から、サイズ10の標本を抽出して、定義通りにカイ二乗値を計算することを10,000回繰り返すシミュレーションを行い、そこからカイ二乗分布をプロットしてみる。まずは母平均が既知であるという前提で計算を行なう。

#平均50, 標準偏差10(分散100)の正規分布を利用
p_mean = 50
p_std = 10
population = stats.norm(loc=p_mean, scale=p_std)

sample_size = 10 #標本サイズ
n_trial = 10000
chi2_array = np.zeros(n_trial)

for i in range(0, n_trial):
    sample = population.rvs(sample_size)

    #定義通りにカイ二乗値を計算する。
    #母平均p_meanは既知という前提で計算に使用
    chi2 = np.sum([((x - p_mean)/p_std)**2 for x in sample])
    chi2_array[i] = chi2

sns.distplot(chi2_array, kde=False, norm_hist = True)
x = np.arange(start = 0, stop = 30, step = 0.1)
plt.plot(x, stats.chi2.pdf(x=x, df=sample_size), label=f'df = {sample_size}')
plt.plot(x, stats.chi2.pdf(x=x, df=sample_size-1), label=f'df = {sample_size-1}')
plt.xlabel("chi2")
plt.ylabel("Frequency")
plt.legend()
plt.show()


母平均を既知として計算に使用しているので、自由度（df）は標本サイズ（今回は10）と等しくなる。実際にシミュレーションで得られたヒストグラムを、自由度10および9の理論的なカイ二乗分布のカーブと重ねてみると、自由度10の方に合致する。


今度は母平均は未知として、標本平均を用いて計算を行う。この場合は自由度が1つ減少する。

#カイ二乗値の計算を行う部分のみ抜粋
for i in range(0, n_trial):
    sample = population.rvs(sample_size)
    s_mean = sample.mean() #標本平均

    #定義通りにカイ二乗値を計算する。
    #今度は母平均は未知という前提で、標本平均s_meanを計算に使用
    chi2 = np.sum([((x - s_mean)/p_std)**2 for x in sample])
    chi2_array[i] = chi2


先程同様に得られたヒストグラムを、自由度10および9の理論的なカイ二乗分布のカーブと重ねてみると、今度は自由度9の方に合致した。

　

ピアソンのカイ二乗検定

例えば、ある製品を生産する工場AとBがあり、不良品の発生個数について以下のようなデータが得られたとする。

不良品 良品
A 780 37220
B 20 1980

工場Aの不良率は約2%、工場Bは約1%だが、これらは有意な差と言えるか？（適当なデータなので、どちらも不良品出し過ぎ！というツッコミは無しでw）

ピアソンのカイ二乗検定で検討する（有意水準は5%とする）。最初にデータのクロス集計表を作る。

data = pd.DataFrame({
    'factory':['A', 'A', 'B', 'B'],
    'quality':['good', 'defective', 'good', 'defective'],
    'quantity':[37220, 780, 1980, 20]
})

cross = pd.pivot_table(
    data=data,
    values='quantity',
    aggfunc=sum,
    index='factory',
    columns='quality' 
)

cross

quality　　defective　　good
factory
A　　　　　780　　　　37220
B　　　　　20　　　　 1980


集計表が出来れば、専用の関数で簡単に検定を行うことが可能である。

#correction=Trueにすると、イェーツの補正という処理が行われる
#度数の極端に小さい項目が、集計表に含まれる場合に適用するようだが、その妥当性については諸説ある模様
#元々の原理通りに検定を行うのであれば、Falseにしておく
chi2, p_value, df, exp_freq_array = stats.chi2_contingency(cross, correction=False)
print(f'カイ二乗値 = {chi2}')
print(f'p値 = {p_value}')
print(f'自由度 = {df}')
print(f'期待度数表\n{exp_freq_array}')

p値は約0.001となり、5%（0.05）を下回るので、工場AとBの不良率には有意な差があると言える。

カイ二乗値 = 10.74
p値 = 0.001048
自由度 = 1
期待度数表
[[ 760. 37240.]
[ 40. 1960.]]


期待度数表について、手計算と比較して確認する。それぞれの合計値を記載した集計表を示す。

不良品 良品 合計
A 780 37220 38000
B 20 1980 2000
合計 800 39200 40000

もし工場A、Bの違いを無視してトータルで見た場合、不良率は800/40000 = 2%である。
このトータルの不良率通りになる場合、それぞれの工場における不良品個数は以下の通りになるはずである。これが期待度数となる。

  • A工場：38000 * 2% = 760個
  • B工場：2000 * 2% = 40個

良品も併せた期待度数表を以下に示す。確かに先程の出力と一致した。

不良品 良品
A 760 37240
B 40 1960


定義通りにピアソンのカイ二乗値も計算してみる。結果は10.74となり確かに先程の出力と一致した。

cross_array = np.array([[780, 37220],[20, 1980]])
exp_freq_array = np.array([[760, 37240],[40, 1960]])
chi2 = 0

for i in range(0, 2):
    for j in range(0, 2):
        chi2 += (cross_array[i][j] - exp_freq_array[i][j]) ** 2 / exp_freq_array[i][j]

print(f'カイ二乗値 = {chi2:.4}')

　

カイ二乗分布を用いた母分散の区間推定

カイ二乗分布を用いて、母分散の区間推定を行ってみる。題材として東京大学教養学部統計学教室 編『基礎統計学I 統計学入門』東京大学出版会の練習問題11.6 ii)を解いてみる。東京における10日間の温度データから、その母分散\sigma^2の信頼区間を信頼係数95%で求める。


#東京大学出版会 統計学入門 問題11.6 ii)より
data = np.array([21.8, 22.4, 22.7, 24.5, 25.9, 24.9, 24.8, 25.3, 25.2, 24.6])
df = data.size - 1
var = data.var(ddof=1)

chi2 = stats.chi2(df = df)

#t分布のときと異なり、カイ二乗値は分母に来るため、その値が大きいほうが下限側になることに注意
lower = df * var / chi2.ppf(1.0 - 0.05/2)
upper = df * var / chi2.ppf(0.05/2)
print(f'信頼区間 [{lower:.4}, {upper:.4}]')

得られた信頼区間は、書籍記載の練習問題の解答ときちんと一致した。

信頼区間 [0.9173, 6.462]

　
interval関数を用いた方法も試してみる。もちろん結果は先程と一致する。

data = np.array([21.8, 22.4, 22.7, 24.5, 25.9, 24.9, 24.8, 25.3, 25.2, 24.6])
df = data.size - 1
var = data.var(ddof=1)

interval = stats.chi2.interval(alpha = 0.95, df = df)

#先程と同様、どちらが上限/下限となるかに注意
lower = df * var / interval[1]
upper = df * var / interval[0]
print(f'信頼区間 [{lower:.4}, {upper:.4}]')

　

等分散性の検定

正規分布に従う2つの群について、母集団の分散が等しいか否かを検証する場合はF検定を行う。ただしScipyのstatsモジュールには、F検定を簡単に直接行える関数は用意されていない模様なので、教科書などを参考に自前で実装してみる。

#F検定を行う関数. 2群のデータをそれぞれ引数で与える.
def ftest(d1, d2):
    var1 = d1.var(ddof=1)
    var2 = d2.var(ddof=1)
    df1 = d1.size - 1
    df2 = d2.size - 1

    #F統計量の計算.常に値が1より大きくなるようにする.
    f_value = var1/var2 if var1 > var2 else var2/var1

    p1 = stats.f.cdf(f_value, df1, df2)
    p2 = stats.f.sf(f_value, df1, df2)
    p_value = min(p1, p2) * 2

    return f_value, p_value

#分散が異なる正規分布から、サイズの異なる2群をランダムに生成して与えてみる.
#なお平均(50)の違いは、当然ながら結果には影響しない.
np.random.seed(1)
data1 = stats.norm.rvs(loc = 50, scale = 5, size = 30)
data2 = stats.norm.rvs(loc = 50, scale = 10, size = 50)

f_value, p_value = ftest(data1, data2)
print(f" F-value = {f_value:.4}, P-value = {p_value:.4}")

結果は以下の通りであり、p値が有意水準5%（0.05）を下回ったので、実際に2群の分散が有意に異なることを検証できた。

F-value = 3.252, P-value = 0.0002677

参考までに、今回の2群をヒストグラムで描いて見ると下図のようになる。


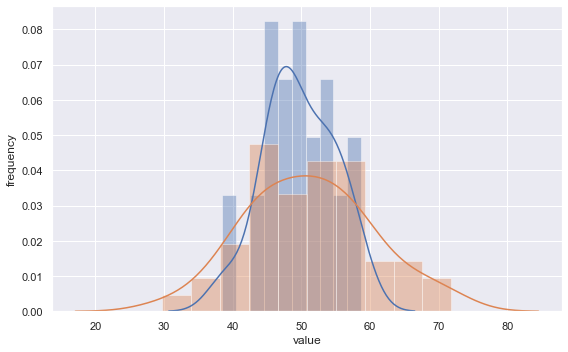
なおstatsモジュールには、実はF検定とは別の、等分散性の検定を行う関数が用意されている（Bartlett検定、Levene検定）。これらは共に、本来は3群以上に対して適用する手法とのことであるが、2群でも適用可能であり、statsモジュールにおいてはF検定ではなくこれらを用いる想定である模様。

これらの原理や使い分けについてはあまり理解出来ていないが（F検定と同様、正規分布に従う2群であればBartlett検定を、そうでない場合はLevene検定を適用する？）、試しに先程F検定を行った2群に対して使用してみる。

#data1, data2は先程F検定を行ったものと同じ
data1 = stats.norm.rvs(loc = 50, scale = 5, size = 30)
data2 = stats.norm.rvs(loc = 50, scale = 10, size = 50)

#先程同様の、自作関数によるF検定
f_value, p_value = ftest(data1, data2)
print(f"Ftest : F-value = {f_value:.4}, P-value = {p_value:.4}")

#Bartlett検定
stat, p_value = stats.bartlett(data1, data2)
print(f"Bartlett : statistics = {stat:.4}, P-value = {p_value:.4}")

#Levene検定
stat, p_value = stats.levene(data1, data2)
print(f"Levene : statistics = {stat:.4}, P-value = {p_value:.4}")

結果は以下の通り。いずれの手法でもp値は有意水準5%（0.05）を下回っている。

Ftest : F-value = 3.252, P-value = 0.0002677
Bartlett : statistics = 10.83, P-value = 0.0009991
Levene : statistics = 8.886, P-value = 0.003831